「群」とは、数字などの数学的な「要素」と、その間に働く「演算子」を持ち合わせた集合の事を云う。群論は、こうした群を扱う数学である。標準理論における対称性の拡張を考える時、この群の概念は重要である。
◇群のルール:整数「…-2、-1、0、1、2、…」と演算子「+」の群の場合
- 0のように、どの要素に作用してもその要素の値を変えない「単位元」がある/例:0+3=3
- どの要素にも「単位元」に戻すような対となる要素が存在する/例:3+(-3)=0
- どの2つの要素同士を作用させて出て来た値も、集合内の要素の1つである/例:3+2=5、5も整数である
- 3つの要素のうち、[1つ目を2つ目に作用させた結果に3つ目を作用させた結果]と、[2つ目を3つ目に作用させた結果に1つ目を作用させた結果]は、一致する/例:(1+2)+3=1+(2+3)=6
以上のように、例えば「奇数」と「演算子(+)」の集合の場合は、群では無いと言える
◇可換群と非可換群の違い
- 例:正三角形の対称性の群
- ※回転操作(時計回り120°回転)を「回」とする
- ※反転操作(左右方向に鏡像反転)を「鏡」とする
- ――元の三角形をe(単位元)とすると、正三角形の対称性は次の6個の要素を持つ群を成している:{e, 回, 回2, 鏡, 鏡回, 鏡回2}
- (ここでは、鏡回=回2鏡, 回鏡=鏡回2)
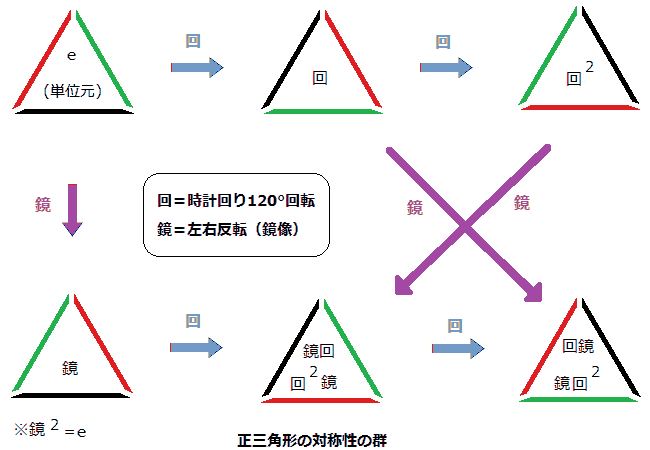
図で見ると分かるように、[鏡回操作を施した正三角形]と[回鏡操作を施した正三角形]は異なる。このように操作の順番を選ぶ群を「非可換群」と呼び、標準理論など量子的な理論を構築するうえで重要な役割を果たす。
◇標準理論~力の統一に伴う群の拡張
標準理論など量子的な理論では、「行列」を要素として持つ群を扱う。一般的には非可換。
ユニタリ群U(n)…nは行列Uが持つ次元。U=「unitary(単元)」の頭文字。
- U(1)…1次ユニタリ群。幾何学的には複素平面上の単位円の回転上の点の集合を表す。要素は1つの成分(偏角θ)のみで表す事ができる。ちなみに、U(1)は回転の順番を変えても結果に影響しないので、「可換群」
- U(2)…2×2の行列によって、2つの成分を、複素2次元空間の中で大きさを変えずに変換
- U(3)…3×3の行列によって、3つの成分を、複素3次元空間の中で大きさを変えずに変換
標準理論では特に「SU(n)」「特殊ユニタリ群」を用いて論じる。S=「Special(特殊)」の頭文字。特殊ユニタリ群SU(n)は、ユニタリ群U(n)の部分群である。複素n次元空間上にある仮想的な立方体(一辺の長さ=1、体積=1)が、回転(変換)後も「体積=1」を保つような特別な変換であるので、「Special-Unitary」。
- SU(n)の自由度=任意に設定できるパラメータ数=n2-1個
- ――SU(2)ではパラメータ3個、SU(3)ではパラメータ8個
- U(1)…例:電磁相互作用(光子、1成分…アイソスピンもカラー荷も持たない)
- SU(2)…例:電子スピン(2成分)、弱い相互作用(弱アイソスピン、2成分)
- SU(3)…例:強い相互作用(カラー荷、3成分)
電磁相互作用、弱い力、強い力を統合した大統一理論GUTを構築する場合は、標準理論における3つの群を統合する⇒SU(3)×SU(2)×U(1)を含む事が必須条件。この拡張された群のうち最小の物がSU(5)。
SU(5)⊃ SU(3)×SU(2)×U(1)
――「電磁相互作用」と「弱い相互作用」を統一⇒「電弱統一理論」
弱い相互作用について「弱アイソスピン」を想定する(これは、強い相互作用において「アイソスピン」を想定したのと同じ手法である)。
電子と電子ニュートリノは、状態が異なるだけで本質は同じ粒子であるとする。「電子=弱アイソスピン下向き」の状態、「電子ニュートリノ=弱アイソスピン上向き」の状態。弱アイソスピン空間内の回転で互いに移り変われると考える。
2種類のフェルミオンのペアの間の相互作用を考えるため、弱アイソスピン2成分を変換するSU(2)を設定する。これにゲージ原理を適用する。そうすると、弱アイソスピンのゲージ理論からは、力を媒介する3つのベクトルボソンが導ける。
次に、対称性を拡張して、弱い力のSU(2)ゲージ場と電磁力のU(1)ゲージ場を結合する。
この拡張されたゲージ対称性は、積の形「SU(2)×U(1)」で書かれる。このゲージ理論からは、光子と3つのウィークボソン(ゲージ粒子)W+、W-、Z0が導かれる。
――標準理論の要「自発的対称性の破れ」…粒子が質量を持つ機構について
電弱統一理論の方程式には、ゲージ粒子の質量を表す項が追加されているが、弱い力のSU(2)ゲージ粒子の質量をうまく説明できない(無限大の困難が生じる上、繰り込み可能な理論になっていない)。
これを解決したのが、「自発的対称性の破れ」いわゆる「ヒッグス機構」である。
「自発的対称性の破れ」とは、ある対称性を持った系が、エネルギー的に安定な真空に落ち着くことで、その対称性が破れる現象の事である。この現象は素粒子理論以前にも発見されている。超電導は「自発的対称性の破れ」で説明できる現象である。
素粒子物理学では、「自発的対称性の破れ」が起きると、必ず質量0、スピン0の粒子が出現する事が示されている。ヒッグス機構は、「このスピン0の粒子が出現する代わりに、その自由度を元々質量0であったゲージ粒子の質量に転換できる」というものである。電弱統一理論は、「ヒッグス機構」を備える事で完成した(ワインバーグ=サラム理論)。
ワインバーグ=サラム理論は、だいたい、以下のような事を記述する。
(1)電子&電子ニュートリノの対(或いはミューオン&ミューニュートリノの対)の運動方程式は、「局所的SU(2)×U(1)ゲージ対称性」を満たしている。この段階では、S(2)の3つのゲージ粒子とSU(1)の1つのゲージ粒子は全て質量0の状態である。
(2)局所的SU(2)×U(1)に、4つの成分を持つヒッグス場を導入する。この4成分は、SU(2)×U(1)のゲージ対称性とゲージ粒子の数を考慮した物である。
(3)ヒッグス場のポテンシャル(滑らかなWのような形)は、中央部分が安定な状態で無いため、ゲージ粒子は、すぐに最も低いエネルギー状態に落ち込んでいく。つまり場は、0以外の値を取る。これが「自発的に対称性が破れた状態」である。
(4)「自発的対称性の破れ」によって、ヒッグス場の4成分のうち、3つがSU(2)の3つのゲージ粒子の質量となり、ヒッグス場の余った成分がヒッグス粒子として残る。元々あったSU(2)×U(1)のゲージ対称性が破れた後は、電磁力のU(1)ゲージ対称性だけが残る。つまり、光子の質量のみが0である。
(5)ゲージ対称性が自発的に破れる前は、カイラル対称性も満たしている状態である(※弱い相互作用は左と右を区別する「カイラル」である。左巻きしか存在しないニュートリノ以外のフェルミオンは、右巻き・左巻きスピン成分が混合した状態=「カイラル対称性」)。ヒッグス場の状態が変わってゲージ対称性が破れる⇒カイラル対称性も破れる。結果として、フェルミオンは質量を持つようになった。
※電子の場合:
左巻きeL、右巻きeRという2つの状態が仮にあるとする。左巻き電子には弱い相互作用が働くので弱電荷を持つ状態になるが、右巻き電子には弱い相互作用が働かないので電荷を持たない。
カイラル対称性を満たしている(質量0)時は、左巻き・右巻きが混じり合っている状態。
このような電子がヒッグス場と相互作用すると、スピン状態が左巻き→右巻き→左巻き…と転移して行く事になるが、これは、「弱電荷が生じたり消えたりする(弱電荷が保存されない)」という過程である。カイラル対称性が破れたために起こる現象である。
このスピン状態の転移が、電子の動き(加速度)に対する抵抗力となり、光速より遅くなる。これが電子の(慣性)質量の起源である。
◇「強い力」の起源~量子色力学
クォークモデルの困難⇒分数電荷の問題、スピンの問題
例:Δ++粒子におけるクォークの組み合わせuuu、Ω-粒子におけるクォークの組み合わせsss
クォークはスピン1/2を持っているので、3つのクォークのスピンは全て同じ向きを向いていなければ、Δ++粒子やΩ-粒子のスピン3/2を構成する事はできない。しかし、クォークはフェルミオンであるので、Δ++粒子やΩ-粒子のスピン3/2に関わるクォークのスピンの向きは、フェルミオンが満たすべき「パウリの排他原理」に反している。
この矛盾を解決するため導入されたのが、3つの「カラー荷」と呼ばれる内部自由度の概念である。カラー荷(赤、青、緑)が組み合わさって白色になった場合のみ、観測可能とする。
これで記述すると、
- Δ++粒子におけるクォークの組み合わせu赤u緑u青
- Ω-粒子におけるクォークの組み合わせs赤s緑s青
となり、スピンが同じでもカラー荷が違うため、同じ状態にはならず、パウリの排他原理を満たしていると解釈できる。
「カラー荷」は3つの自由度を持つ事から、SU(3)対称性に基づくクォークのゲージ理論を構築できる。このゲージ理論から導かれる「力の媒介粒子(ゲージ粒子)」が、「グルーオン(質量0)」である。
SU(3)のパラメータは8個であるから、8種のグルーオンが存在する筈であるが、赤、緑、青のカラー荷を持つため、クォークと同じように、直接には観測に掛からない。
――量子色力学から導かれる「クォークの閉じ込め」
クォーク同士を引き剥がした場合、電磁力とは違い、「強い力」は距離と共に減衰せず一定値を保つ。従って、クォークを引き剥がすために投入されるエネルギーは、クォークの距離と共に増大し、真空から新たにクォーク・反クォークのペアを作り出すエネルギーになる。新たに生成されたクォーク・反クォークのペアは、引き剥がされたクォークとカラー荷の総和が白色となるように結び付き、新たなハドロンのペアとなる。
これが「クォークの閉じ込め」である。このため、グルーオンは無限大まで到達する事ができず、核の外には働かなくなる。
――量子色力学から導かれる「漸近的自由性」
クォーク同士が近づくにつれ、その間に働く力は弱くなる。無限小の距離では力は全く働かなくなる。すなわち、核の中のクォークは、力に束縛される事なく自由に動き回っている状態である。
★標準理論が抱える問題…大統一理論GUT(=電磁力、弱い力、強い力の統一理論)は、まだ完成しているとは言えない。
- ※標準理論の正確さを検証するため、ハイパーカミオカンデで陽子崩壊の観測が計画されている
- http://www.hyper-k.org/physics/phys-protondecay.html
◇ヒッグス粒子の質量に関する根源的な謎
重力を統合する際の「階層性問題」に関わる。量子重力に関わるプランクエネルギーのスケール~1019GeVと電弱統一エネルギーのスケール~102GeVとの間には、1017ものスケールの乖離がある。
このような大きすぎるエネルギースケールの乖離を扱うのは、困難が伴う。これが「階層性問題」である。
最近の実験でヒッグス粒子の質量は125GeVと求められている。これを標準理論に投入してヒッグス粒子の質量の高次補正を求めようとすると、標準理論が扱えるエネルギー限界を超えてしまうのである(発散)。
つまり、ヒッグス粒子の質量は、量子重力理論のような根源的なレベルで無いと、高次補正を加えた理論値を弾き出せない事を示している…と見えるのである。
しかし、プランクエネルギーのスケール1019GeVから、一気にヒッグス粒子質量125GeVに収束するような――1017ものエネルギースケールの乖離を解消するような物理学的なプロセスがあるのかどうかは、今でも分かっていない。
現在時点では、数学的には、標準理論を高エネルギーレベルまで拡大した改良版=SU(5)ゲージ対称性を満たす超対称性理論(supersymmetry,SUSY)が有望視されている。
◇その他の謎…重力の謎、消えた反物質の謎(この宇宙には、何故、物質しか残っていないのか)、暗黒物質や暗黒エネルギーの正体
量子重力理論、超ひも理論、ブレーン理論など、幾つかの候補が考案されている。
